Tableau De Variation Polynome Du Second Degré

Ah, les polynômes du second degré ! On dirait une équation ennuyeuse à apprendre au lycée, n'est-ce pas ? Détrompez-vous ! Derrière cette formule un peu barbare se cache un outil super puissant pour comprendre et modéliser le monde qui nous entoure. Et le tableau de variation, c'est un peu la carte au trésor qui nous guide à travers les méandres de ces polynômes. Alors, prêt à partir à l'aventure ?
Mais au fait, c'est quoi un polynôme du second degré ? C'est une expression de la forme ax² + bx + c, où a, b, et c sont des nombres. Pensez à la trajectoire d'une balle de basket (enfin, si on néglige la résistance de l'air!), à la forme d'une arche, ou même à la courbe de vos profits si vous êtes un entrepreneur ambitieux. Tous ces phénomènes peuvent être approximés par un polynôme du second degré.
Alors, pourquoi s'embêter avec un tableau de variation ? Simplement parce qu'il nous donne une vue d'ensemble de la fonction ! Imaginez que votre polynôme représente les profits de votre entreprise. Vous voulez savoir quand vos profits sont les plus élevés, n'est-ce pas ? Le tableau de variation vous dit :
- Si la fonction croît (vos profits augmentent) ou décroît (vos profits diminuent).
- Où se situe le maximum (le pic de vos profits) ou le minimum (le point le plus bas).
En gros, le tableau de variation est un résumé visuel et super pratique de l'évolution de votre polynôme. Il est beaucoup plus simple de comprendre l'évolution de la fonction en regardant ce tableau qu'en essayant de deviner à partir de la formule brute !
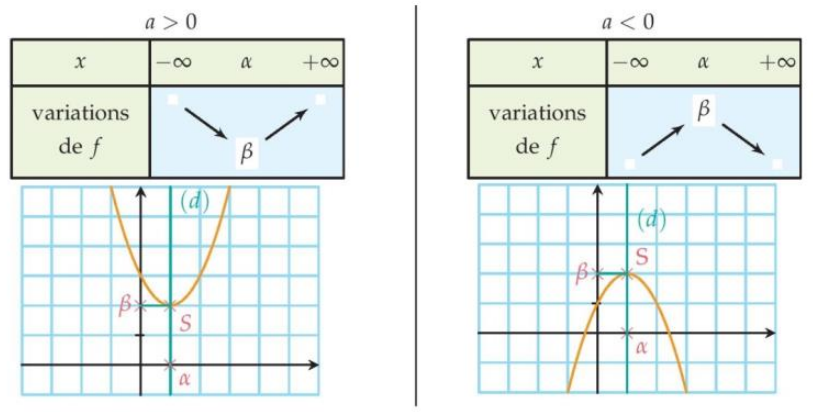
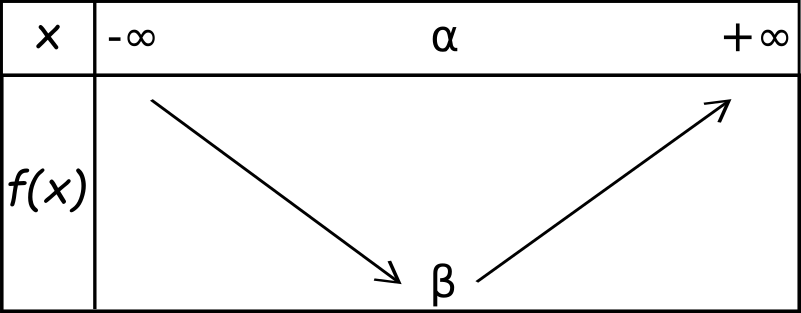
Comment on construit ce tableau magique ? C'est assez simple ! La clé, c'est de trouver le sommet de la parabole (la forme du polynôme du second degré) et son axe de symétrie. La formule pour trouver l'abscisse du sommet est -b/2a. Ce point marque le tournant de la fonction : soit elle croît avant, puis décroît après, soit l'inverse. Ensuite, on regarde le signe de 'a'. Si 'a' est positif, la parabole a la forme d'un 'U' (elle sourit !), et le sommet est un minimum. Si 'a' est négatif, la parabole a la forme d'un '∩' (elle est triste !), et le sommet est un maximum.
Une fois qu'on a ces informations, on peut remplir le tableau de variation. On indique les valeurs de x (de moins l'infini à plus l'infini), l'abscisse du sommet, et les flèches qui indiquent si la fonction croît ou décroît. On ajoute également la valeur de la fonction au sommet. Et voilà, le tour est joué !
Alors, la prochaine fois que vous croiserez un polynôme du second degré, n'ayez pas peur ! Pensez au tableau de variation comme à un guide, un GPS mathématique qui vous aidera à comprendre son comportement et à en tirer des conclusions utiles. C'est beaucoup plus fun qu'il n'y paraît, promis !